समविभव पृष्ठ क्या है – Samvibhav Prasth Kise Kahte Hai :

” किसी वैद्युत क्षेत्र में खींचा गया वह पृष्ठ जिस पर स्थित सभी बिंदुओं पर विद्युत विभव बराबर हो सम विभव पृष्ठ कहलाता है। “

दूसरे शब्दों में सम विभव पृष्ठ पर किन्हीं दो बिंदुओं के बीच विद्युत विभवांतर सदैव शून्य ही होता है ।अतः किसी आवेश को सम विभव पृष्ठ के एक बिंदु से दूसरे बिंदु तक लाने में कोई कार्य नहीं करना पड़ता ।

परंतु यह तभी संभव है जब कि वैद्युत आवेश को वैद्युत क्षेत्र के लंबवत ले जाया जाए। अतः सम विभव पृष्ठ प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा के लंबवत ही होता है ।विद्युत क्षेत्र में भिन्न-भिन्न बिंदुओं पर क्षेत्र की दिशा बल रेखाओं द्वारा प्रदर्शित की जाती है ।

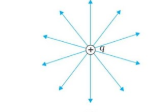
किसी एकल आवेश q के लिए विभव नीचे दी हुई समीकरण के द्वारा बताया गया है-V = kq/r ( जहां k = 1/(4(pi)e0) है )

इससे यह प्रकट होता है कि यदि r नियत है तो V नियत रहता है। इस प्रकार किसी भी एकल आवेश के लिए समविभव पृष्ठ संकेंद्रित गोले होते हैं जिनके केंद्र पर वह आवेश स्थित होता है।

समविभव पृष्ठ के गुणधर्म – Properties of Equipotential Surface in Hindi:

1. हमने विभवांतर में पढ़ा था की विभवान्तर उस कार्य के बराबर होता है जो एक बिंदु से दूसरी बिंदु अर्थात निम्न विभव बिंदु से उच्च विभव बिंदु तक लाने में करना पड़ता है।

V_AB = W_AB = V_A – V_B

A पर विभव V_A तथा B पर विभव V_B तो विभवान्तर

चूँकि हमने समविभव की परिभाषा में पढ़ा की इस पृष्ठ पर सभी बिंदुओं पर विभव का मान समान होता है अर्थात

V_A = V_B

अतः कृत कार्य

W_AB = 0

अर्थात समविभव पृष्ठ पर स्थित किसी बिन्दु से अन्य बिंदु तक ले जाने में कोई कार्य नहीं करना पड़ता।

2. हम जानते है की किसी एकांक धन आवेश को dl दूरी तक विस्थापित करने में किया गया कार्य निम्न सूत्र द्वारा दिया जाता है।

dW = E.dlCosθ

चूँकि ऊपर हमने देखा की समविभव पृष्ठ पर एक जगह से दूसरी जगह जाने में (विस्थापन) कोई कार्य नहीं करना पड़ता अर्थात कृत कार्य शून्य होता है

अतः

dW = E.dlCosθ = 0

यहां E तथा dl तो शून्य संभव नहीं है

अतः Cosθ = 0

θ = 90

अर्थात समविभव पृष्ठ में E (विद्युत क्षेत्र ) तथा dl (विस्थापन ) के मध्य 90 डिग्री का कोण बनता है अर्थात विद्युत क्षेत्र समविभव पृष्ठ के लंबवत होता है।

समविभव पृष्ठ के उदाहरण:

1. माना किसी विलगित आवेश के +q के कारण r दूरी पर विद्युत विभव का मान

यदि इस +q आवेश के चारो ओर r त्रिज्या का गोलीय पृष्ठ बनाया जाए तो इस गोलीय पृष्ठ के सभी बिंदुओं पर विभव का मान समान होगा अर्थात समविभव पृष्ठ गोलीय आकार का हो सकता है जिसका केंद्र +q आवेश होगा।

2. यदि x दिशा में विद्युत क्षेत्र E है तो x के लंबवत रखा समतल पृष्ठ समविभव पृष्ठ होता है। 3. चित्रानुसार समविभव पृष्ठ समान प्रकृति व परिमाण के आवेश युग्म मिलकर बनाते है।     यदि यह नोट्स आपको स्टडी में उपयोगी साबित हुए है तो आप इन्हे अपने Classmates & Friends के साथ Share कर सकते है |