निलंबित कुण्डली धारामापी (suspended coil galvanometer in Hindi ) :
बनावट या संरचना (Construction) :
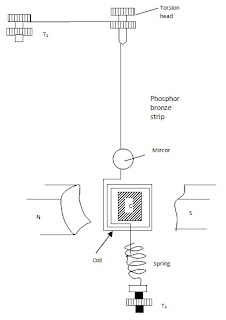
निलम्बित कुण्डली धारामापी की संरचना चित्र में दिखाई गयी है , इसमें एक अनुचुम्बकीय धातु (एल्युमिनियम) पर विद्युत रोधी तथा ताँबे के तार को लपेटकर कुण्डली बनाई जाती है।
इस कुण्डली को फॉस्फर ब्रॉन्ज (phosphor bronze) के तार की सहायता से दो प्रबल चुम्बकों के मध्य लटकाया जाता है।
कुण्डली के भीतर एक नरम लोहे की क्रोड़ रखी रहती है।
कुंडली का एक सिरा मरोड़ कुंजी (Torsion hand) से होता हुआ संयोजक पेच T1 से जुड़ा रहता है , यहाँ मरोड़ कुंजी (Torsion hand) कुण्डली को आवश्यकता पड़ने पर घूमने के लिए स्वतंत्र रखता है।
मरोड़ कुंजी तथा कुण्डली के मध्य फॉस्फर ब्रॉन्ज तार पर एक समतल दर्पण लगा रहता है जो तार के साथ आसानी से घूम सकता है।
यह दर्पण लैम्प व स्केल व्यवस्था द्वारा विक्षेप अध्ययन करने अर्थात देखने के काम आता है।
कुण्डली का नीचे वाला सिरा एक प्रत्यास्थ स्प्रिंग से जुड़ा रहता है तथा यह स्प्रिंग T2 से जुडी रहती है।
निलंबित कुण्डली धारामापी का सिद्धान्त:
यह युक्ति इस सिद्धांत पर कार्य करती है कि ” जब किसी धारावाही कुण्डली को किसी समान या समरूप चुम्बकीय क्षेत्र में रखा जाए और इसमें धारा प्रवाहित की जाये तो कुंडली पर एक एक बल आघूर्ण कार्य करता है जो कुण्डली को घुमाता है तथा यह घूर्णन विक्षेप (बल आघूर्ण) कुण्डली में प्रवाहित धारा के मान पर निर्भर करता है “
माना कुंडली में n फेरे लिपटे हुए है , क्षेत्रफल A , चुम्बकीय क्षेत्र B , तथा कोण θ है तो
बल आघूर्ण
T = nIAB sinθ
यदि चुम्बकीय क्षेत्र त्रिज्य है तो θ = 90′
अतः
T = nIAB
इस बल आघूर्ण के कारण कुण्डली घूमने लगेगी फलस्वरूप फॉस्फर ब्रॉन्ज़ तार में ऐंठन आने लगेगी
माना फॉस्फर ब्रॉन्ज़ (phosphor bronze) तार में ऐंठन कोण ϴ है तो
ऐंठन बल युग्म
Tr = Cϴ
यहाँ ध्यान दे की यह ऐंठन बल युग्म , बल आघूर्ण के विपरीत लगता है
यदि दोनों बल बराबर होंगे तो इसे संतुलन की स्थिति कहते है अतः सन्तुलन की स्थिति में
ऐंठन बल युग्म = बल आघूर्ण
Cϴ = nIAB
अतः
I = Cϴ / nAB
यहाँ C/ nAB को परिवर्तन गुणांक k कहते है
अतः I = kϴ
त्रिज्य क्षेत्र (Radial Field in Hindi):
त्रिज्य क्षेत्र का अभिप्राय है कुण्डली के क्षेत्रफल (A) तथा चुम्बकीय क्षेत्र (B) एक दूसरे के लंबवत है अर्थात क्षेत्रफल A तथा चुंबकीय क्षेत्र B के मध्य 90 डिग्री का कोण है। इस स्थिति को ही त्रिज्य क्षेत्र कहते है।
इस स्थिति में धारामापी की सुग्राहिता अधिक होती है।
कार्यविधि:
जैसा की हमने देखा की इसमें लगा दर्पण का उपयोग कर हम कुण्डली में हुआ विक्षेप ज्ञात करते है। यहाँ विक्षेप ϴ मान रहे है।
जब तार में लगे दर्पण में ϴ कोण विक्षेप उत्पन्न होता है तो इस स्थिति में दर्पण में आपतित प्रकाश किरण का परावर्तन हो जाता है अतः परावर्तित होने से 2ϴ कोण घूम जाती है।
यदि स्केल पर प्रकाश बिंदु का विस्थापन d प्राप्त होता है तथा दर्पण से स्केल के मध्य की लंबवत दुरी D है तो
tan(2ϴ) = d/D
Remark:
दोस्तों अगर आपको इस Topic के समझने में कही भी कोई परेशांनी हो रही हो तो आप Comment करके हमे बता सकते है | इस टॉपिक के expert हमारे टीम मेंबर आपको जरूर solution प्रदान करेंगे|