शुद्ध धारितीय परिपथ में प्रत्यावर्ती वोल्टता तथा प्रत्यावर्ती धारा के मध्य कला संबंध तथा फेजर आरेख

शुद्ध धारितीय परिपथ में प्रत्यावर्ती वोल्टता तथा प्रत्यावर्ती धारा के मध्य कला संबंध तथा फेजर आरेख  :

पहले हम बात करते है की जब किसी संधारित्र को जब किसी दिष्टकारी स्रोत से जोड़ा जाता है तो संधारित्र की एक प्लेट धनावेशित हो जाती है तथा दूसरी प्लेट ऋणावेशित हो जाती है तथा दोनों प्लेटो के मध्य विभवान्तर उत्पन्न हो जाता है , यह क्रिया तब तक होती रहती है जब तक की प्लेटों के मध्य उत्पन्न विभवांतर आरोपित विभवान्तर के बराबर न हो जाए। बराबर होने के पश्चात् परिपथ में धारा रुक जाती है।
लेकिन जब संधारित्र से कोई प्रत्यावर्ती स्रोत को जोड़ा जाता है तो यह आवेशन वाली क्रिया होती है और दोनों प्लेटे आवेशित हो जाती है जिससे एक प्लेट धनावेशित हो जाती है तथा दूसरी प्लेट ऋणावेशित हो जाती है और इन दोनों प्लेटों के मध्य एक विभवान्तर उत्पन्न हो जाता है।

प्रत्यावर्ती स्रोत लगाने पर यह प्रक्रिया लगातार होती रहती है क्यूंकि प्रत्यावर्ती धारा में स्रोत की ध्रुवता लगातार बदलती रहती है जिससे प्लेटों की ध्रुवता भी लगातार बदलती रहती है और परिपथ में लगातार धारा बहती रहती है। अत: संधारित्र प्रत्यावर्ती धारा में कोई बाधा नहीं डालता है और एक सुचालक की भांति व्यवहार करता है।
क्यूंकि प्रत्यावर्ती स्रोत लगाने से संधारित्र की प्लेटे लगातार आवेशित तथा अनावेषित होती रहती है जिससे प्लेटों के मध्य एक विभवान्तर उत्पन्न हो जाता है यह विभवान्तर परिपथ में धारा के प्रवाह का विरोध करता है या रुकावट डालता है , संधारित्र द्वारा डाली गयी इस रुकावट या विरोध को धारितीय प्रतिघात कहते है , इसे X_c द्वारा व्यक्त किया जाता है तथा इसका मात्रक ओम (‎Ω) होता है।

माना परिपथ में आरोपित वोल्टता का मान निम्न है
V = V_msinwt
माना t समय में संधारित्र पर q आवेश संचित हो जाता है अत:  
q =  CV
यहाँ V का मान रखने पर
q = C V_msinwt
हम जानते है की परिपथ में प्रवाहित धारा
i = dq/dt
यहाँ q का मान रखने पर
i = d(C V_msinwt)/dt
अवकलन हल करने पर

यहाँ X_c = 1 /cw , इसे धारितीय प्रतिघात कहते है।
यहाँ सूत्र समीकरण को देखकर हम स्पष्ट रूप से यह कह सकते है की संधारित्र में प्रत्यावर्ती धारा विभवान्तर से कला में π/2 आगे है
धारा तथा विभवान्तर में कला सम्बन्ध को निम्न प्रकार ग्राफीय रूप में निरुपित करते है।

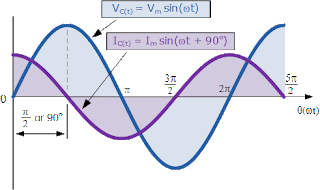
इसे ही फेसर डायग्राम के रूप में निम्न प्रकार निरूपित किया जा सकता है

Remark:

दोस्तों अगर आपको इस Topic के समझने में कही भी कोई परेशांनी हो रही हो तो आप Comment करके हमे बता सकते है | इस टॉपिक के expert हमारे टीम मेंबर आपको जरूर solution प्रदान करेंगे|